Thursday, December 5, 2013
Graphing quadratic functions foldable
Nothing too fancy or mind-shattering here, but perhaps someone may find this useful. Just a quick, little graphic organizer for the steps I want students to follow to make a nice graph of a quadratic function.
Wednesday, December 4, 2013
Group success!!
Today had one of those class periods. You know the ones. Where everyone is working and discussing and arguing and engaged and I'm? I'm just there. Totally and completely unnecessary to the workings of my class. Amaze.
Today was the first day of learning to solve systems by substitution. We went through an example together using @cheesemonkeysf's patented "substitution by stars" method. Then, I passed out some problems for them to work through, telling them to work with their group members and only go to the next problem when everyone in the group was totally good with the previous one. There were some where students had to apply the distributive property and some where they had to isolate a variable first. We had not talked about these. I did not stop class to discuss and fix and give hints, just circulated the room and looked on. Not one kid asked me for help for the 20 minutes that they worked - they puzzled through and argued and made mistakes and erased them and made some more and eventually figured it out all on their own. Holy wow. You guys get it. We all want group work to go exactly like this, but it so rarely does.
Today was the first day of learning to solve systems by substitution. We went through an example together using @cheesemonkeysf's patented "substitution by stars" method. Then, I passed out some problems for them to work through, telling them to work with their group members and only go to the next problem when everyone in the group was totally good with the previous one. There were some where students had to apply the distributive property and some where they had to isolate a variable first. We had not talked about these. I did not stop class to discuss and fix and give hints, just circulated the room and looked on. Not one kid asked me for help for the 20 minutes that they worked - they puzzled through and argued and made mistakes and erased them and made some more and eventually figured it out all on their own. Holy wow. You guys get it. We all want group work to go exactly like this, but it so rarely does.
But finally!! All of the working on norms and redirecting questions with, "Have you asked your group yet?" or "Is this a group question?" and biting my lip to avoid butting in have paid off and there was just this amazing energy and focus and I was so, so proud. Cause there aren't that many glorious classroom moments like this, and it's so easy to focus on all the ways that we aren't perfect and they aren't either. So I want to stop and acknowledge that today was exactly right and keep it in my memory bank for when I'm feeling frustrated and disgruntled. Hooray!!!!
Sunday, December 1, 2013
Axis of symmetry for a quadratic function
My two-year Algebra course is just starting our study of quadratics. So far, we've looked at graphs and tables for quadratic functions and compared them to linear functions and talked about the symmetry of the shape and finding the axis of symmetry from the x-intercepts and finding the reflections of points across the axis of symmetry. I would like students to derive the formula for the axis of symmetry: 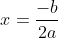 for the quadratic function
for the quadratic function  . The Exeter Math 1 curriculum does this by having students graph functions in the form
. The Exeter Math 1 curriculum does this by having students graph functions in the form  , then generalizing the idea that one of the x-intercepts is zero and the other one is
, then generalizing the idea that one of the x-intercepts is zero and the other one is 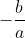 . I created a worksheet that extends on this idea using desmos to graph and having students also derive the formula for the axis of symmetry by averaging the two x-intercepts to get
. I created a worksheet that extends on this idea using desmos to graph and having students also derive the formula for the axis of symmetry by averaging the two x-intercepts to get 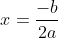 . Then, just like in the Exeter packet, I will have students compare graphs of
. Then, just like in the Exeter packet, I will have students compare graphs of  to graphs of
to graphs of  to realize that the axis of symmetry is not changed by adding a c value to the equation. I'm hoping that the logical progression of the graphs will make sense and that the questions are open enough for this to be genuinely based on student thinking and discovery, but with enough structure that students who are not necessarily used to deriving formulas will have something concrete to think about and answer. Any and all feedback welcome!!
to realize that the axis of symmetry is not changed by adding a c value to the equation. I'm hoping that the logical progression of the graphs will make sense and that the questions are open enough for this to be genuinely based on student thinking and discovery, but with enough structure that students who are not necessarily used to deriving formulas will have something concrete to think about and answer. Any and all feedback welcome!!
Friday, November 22, 2013
Baby steps
There was a good discussion recently on Twitter about complex tasks and why many teachers and students shy away from engaging with them or give up in frustration and return to low-level tasks.
I think that we can all come up with reasons why it's difficult for many teachers (including myself) to move out of their comfort zones and implement rich tasks in their classrooms. I am also interested in figuring out why students would resist complex tasks. @MathEdnet blogged about the various reasons that complex tasks can empower students by giving them more control and a voice as mathematicians and doers. The idea is that working with rich problems allows students to see their knowledge as valuable and themselves as active users of such knowledge. In implementing such tasks in the classroom, however, I have often seen student frustration and discomfort with the change in expectations from previous classes or from how the class had been functioning. This is sometimes especially true for students who care about their progress the most and who have certain ways of doing mathematics that have worked for them in the past that no longer work in a framework of complex problem solving. For these students, complex tasks appear confusing, unfamiliar, and an obstacle to their goal of doing well in the class. It can feel very frustrating to the teacher, especially if she hopes that implementing a complex task will increase student buy-in and engagement. Everybody is unhappy.
There are many ways of working on this issue, I think, and each is unique to the particular confluence of school, teacher, and group of students. Some teachers have big enough personalities that they can persuade students to trust them and step out of their comfort zones through sheer awesomeness.
Teachers like me who have a hard time not being liked by our students and are not inspiring enough to get everyone to drink the Kool Aid come up with more gentle approaches. Baby steps, if you will. I have been working on a mix of traditional and complex instruction that takes students from the type of work that they're used to doing in math classes and gradually, inserts some open problems, starting with smaller tasks that are worked on in class and give students plenty of supports to hopefully build on more and more rich problems as students' comfort level increases.
I am, by no means, amazing at this. I definitely give tasks that are too open for students to handle and they freak out. Or alternatively, too many low-level tasks, which undo some of the work I've put into pushing them past that point. But this is the type of thing that is really, really hard to learn to do. Or, at least, it is for me. It's not something that is part of a graduate course or can be picked up by watching a lesson or two taught by a master teacher. And I have certainly never seen a pre-made curriculum that does this type of nuanced dance between what this particular group of students is comfortable doing and something that's just a bit outside of their comfort and ability zone so that they feel challenged and interested, but not overwhelmed and frustrated or bored and disengaged. So. My point. I did have one. I feel like lots of us on Twitter are stabbing away at this teaching thing, but with different tools, personalities, and kids. And it's easy to feel frustrated that I'm not doing amazing open tasks every day with my students or month-long cross-curricular projects that empower and engage them to the utmost.
But, I'm working just outside of my comfort zone and pushing my students to do the same. Baby steps. But progress, nonetheless. And I'm confident that y'all are doing the same, in your own way.
Thoughts/critiques of this framework? pic.twitter.com/vsTdBKbOhC
— Geoff Krall (@emergentmath) November 20, 2013
I think that we can all come up with reasons why it's difficult for many teachers (including myself) to move out of their comfort zones and implement rich tasks in their classrooms. I am also interested in figuring out why students would resist complex tasks. @MathEdnet blogged about the various reasons that complex tasks can empower students by giving them more control and a voice as mathematicians and doers. The idea is that working with rich problems allows students to see their knowledge as valuable and themselves as active users of such knowledge. In implementing such tasks in the classroom, however, I have often seen student frustration and discomfort with the change in expectations from previous classes or from how the class had been functioning. This is sometimes especially true for students who care about their progress the most and who have certain ways of doing mathematics that have worked for them in the past that no longer work in a framework of complex problem solving. For these students, complex tasks appear confusing, unfamiliar, and an obstacle to their goal of doing well in the class. It can feel very frustrating to the teacher, especially if she hopes that implementing a complex task will increase student buy-in and engagement. Everybody is unhappy.
Not a teacher, but would probably be an awesome one.
Teachers like me who have a hard time not being liked by our students and are not inspiring enough to get everyone to drink the Kool Aid come up with more gentle approaches. Baby steps, if you will. I have been working on a mix of traditional and complex instruction that takes students from the type of work that they're used to doing in math classes and gradually, inserts some open problems, starting with smaller tasks that are worked on in class and give students plenty of supports to hopefully build on more and more rich problems as students' comfort level increases.
I am, by no means, amazing at this. I definitely give tasks that are too open for students to handle and they freak out. Or alternatively, too many low-level tasks, which undo some of the work I've put into pushing them past that point. But this is the type of thing that is really, really hard to learn to do. Or, at least, it is for me. It's not something that is part of a graduate course or can be picked up by watching a lesson or two taught by a master teacher. And I have certainly never seen a pre-made curriculum that does this type of nuanced dance between what this particular group of students is comfortable doing and something that's just a bit outside of their comfort and ability zone so that they feel challenged and interested, but not overwhelmed and frustrated or bored and disengaged. So. My point. I did have one. I feel like lots of us on Twitter are stabbing away at this teaching thing, but with different tools, personalities, and kids. And it's easy to feel frustrated that I'm not doing amazing open tasks every day with my students or month-long cross-curricular projects that empower and engage them to the utmost.
Wait, this isn't what your classroom looks like every day?
But, I'm working just outside of my comfort zone and pushing my students to do the same. Baby steps. But progress, nonetheless. And I'm confident that y'all are doing the same, in your own way.
So coming back to the original question - perhaps what I'm hoping for is more recognition of baby steps and meeting people where they are, both teachers and students, to help them make small, but noticeable progress, as a way out of the cycle that @emergentmath described.
Sunday, October 27, 2013
Getting students to dig deeper into rich problems
So I was going to participate in the #MTBoS Challenges, but then, life happened. I did write a blog post responding to the first challenge, and even though I'm not participating in the full scope of challenges, I'd like to post what I can. So here is what I wrote in response to the question "What is one of your favorite open-ended/rich problems? How do you use it in your classroom?"
I gave students 20 minutes in class to start working on the problem (5 minutes alone, then 15 minutes with their group members) and a week and a half to complete their write-ups. I also met with students individually who were struggling.
Even though we were directed to write about a favorite rich problem, I’m going to write about a problem that is the most recent one that I’ve done with a class because I’m having some issues with the way it’s worked out and would love some feedback on how to make it better.
The problem that I recently gave my 2-year Algebra students (these are 8th graders in the second year of a 2-year course that covers a standard Algebra 1 curriculum) was the first one in the Integrated Math Program, Year 1 book, called Broken Eggs. This was students’ first problem of the week, in which they are to write up their problem-solving process and justify their thinking and solution, if they find one. In this problem, you are told that a number of eggs when put into groups of 2, 3, 4, 5, or 6 always had one egg left over, but fit perfectly into groups of 7. Students were asked to determine whether there was only one unique solution or whether there were many possible solutions, and if so, how they were connected to each other.
Full problem:
I gave students 20 minutes in class to start working on the problem (5 minutes alone, then 15 minutes with their group members) and a week and a half to complete their write-ups. I also met with students individually who were struggling.
I thought that the problem was a good one with which to start as it could be approached from a variety of angles and would encourage for the looking of patterns. However, the results were pretty disappointing. Most kids were only able to find the first solution and did so using brute force (writing out the multiples of seven and testing each one to see how it divided by 2, 3, 4, 5, and 6). Quite a few kids just looked at numbers that weren’t evenly divisible rather than looking for a specific remainder. Almost no one found any other solutions and not a single student found a pattern between the solutions. Almost no students even attempted to find one. So the problem just turned into one that required some organization to keep track of things, but almost no algebraic thinking. So basically, the result was a lot of annoying calculations with little payoff.
I am trying to think about what I could have done differently to encourage students to keep going and to notice patterns that would make their work easier. Having students share strategies maybe would have helped to disseminate some of the shortcuts that a few of the students discovered, but not ones that no one figured out. I think that part of the tension for me is that I want open problems to really be about students’ thinking and approaches, but also be a learning opportunity that stretches them past their current abilities and into something more advanced, and I don’t know how to do that without giving hints or telling kids to change their approach. Basically, I want them to learn and be stretched mathematically, but have it be organic and come as an extension of their own thinking rather than a top-down approach where I direct them.
Part of the issue also is that kids are mostly to work on problems of the week outside of class so I’m not getting much of a chance to see their thinking before they turn them in to me. So another change that I’m thinking of doing is having students turn in a “rough draft” that I can give them feedback on or that we can confer about in person before they complete their write-up. There is a thin line between pushing a student’s thinking and directing it onto a predetermined path that takes away from the problem’s openness and richness, and I am still navigating how to do this in an optimal way. Suggestions welcome!
Part of the issue also is that kids are mostly to work on problems of the week outside of class so I’m not getting much of a chance to see their thinking before they turn them in to me. So another change that I’m thinking of doing is having students turn in a “rough draft” that I can give them feedback on or that we can confer about in person before they complete their write-up. There is a thin line between pushing a student’s thinking and directing it onto a predetermined path that takes away from the problem’s openness and richness, and I am still navigating how to do this in an optimal way. Suggestions welcome!
Thursday, April 25, 2013
Whiteboarding wins and fails
Now that whiteboarding (my posts on it here, here, and here) has become a full-fledged part of my classroom, I wanted to reflect on how it's been going. So first, the successes...
Whiteboarding wins:
Whiteboarding wins:
- Student cooperation and engagement in group activities has been kicked up a notch. I thought that I was doing fine with structuring group work and encouraging student engagement and participation, but whiteboarding has really increased cooperation and discourse between students. There's something about having one person write for everyone that creates more investment in the process and final product. A white board also encourages larger and clearer writing, making it easier for everyone in the group to see and participate.
- All students have to demonstrate understanding and it's harder to hide or have one person do all of the work. When groups present or when I go around the room and talk to groups, I pick students at random to explain their group's thinking. Rotating the marker between group members also help keep everyone involved.
- Kids love to get picked to show their work and work harder to make their thinking more explicit and clear.
- It results in greater perseverance and willingness to try crazy things - something about the ease of erasing makes kids more willing to take risks and get messy with a problem.
- Kids get used to asking questions of others' work and disagreeing with their process politely, and I am seeing this carry over into non-whiteboarding work.
- Students really like it, and it lends itself to other activities & structures that allow it to continue feeling fresh and exciting.
... and now for some failures...
Whiteboarding fails:
- Annoyingly, kids are still uptight about making mistakes and having errors publicly attributed to them. Even after playing the Mistake Game, kids were still getting upset and unhappy with each other when unintentional mistakes would get exposed in front of the class. I had one incident where a group of boys exploded with accusations about whose fault the mistake was and had to talk to them out in the hallway about their behavior. Kids still find it embarrassing to be wrong, which I am finding frustrating. Like, how many times do I have to say, "This is the awesomest, most interesting mistake ever! We are learning so much more from it than we would from the "correct" approach!" before it sinks in? When I would ask groups to present, kids would still anxiously ask "but is it right or wrong?" Right now, I'm working around this by putting up boards with mistakes and having the class give feedback without attributing from which group the mistake came, but I'd like to get to a place where students are actually comfortable with their errors and aren't embarrassed by having them publicly discussed.
- Kids are still kind of bad at asking questions rather than just pointing out the mistakes. Or their questions are really just statements with a lilt at the end: "Should you get 8 when you square 4?"
- The boards are sometimes hard to display if the group wrote too small, and the whiteboard is too big to stick under the document camera. My workaround has been to take a photo of the whiteboard and send it to the projector where I can zoom in on their work. Hopefully, their writing will get better as we continue to use whiteboarding regularly.
- Students would like to have notes they can take home, and whiteboarding does not lend itself to that. I thought Bowman's post on giving students time at the end of a period spent whiteboarding to reflect and write down some notes was really great, but it's hard to find the time for this what with going over homework, whiteboarding, and student explanations of their work, all of which must fit into a 45 minute period, 4 days per week. I've thought about taking photos of their whiteboards and putting them on our class webpage and perhaps asking them to do some reflecting and summarizing for homework, but haven't actually followed up on this.
Overall, I am really happy with how whiteboarding has gone this year!!
Saturday, February 9, 2013
Thoughts on homework
It has sort of taken over my teaching life. We spend a lot of time on it in class, and I spend a lot of time on it outside of class. I am not sure if this is good or bad. The way that I do homework, students have all of the answers and must check their assignment and identify problems they have done incorrectly or that they don't know how to do. In class, students discuss their questions with each other in groups for about 5 minutes, then we make a list of questions to go over as a class. Students volunteer to present their solutions to the identified questions and answer any follow up questions from classmates. Those who got those questions wrong or didn't complete them are expected to make corrections to their work. The whole thing takes about 20 minutes, on average, which is almost half of the 45 minute class period. For my end, I look at each problem for each kid and write feedback on each paper. If there are errors or incomplete work or misunderstandings demonstrated, credit is reduced and students are expected to correct those assignments and turn them back in to me. Once the assignment meets my criteria for "goodness," full credit is given. Students are also required to write up corrections and explanations of their errors for tests and complete a journal entry reflecting on their progress each chapter. For my four classes, which have four homework assignments each week, the whole grading process takes me on average about 2 hours every day. That's a lot of time!!!
On the plus side, I think doing problems independently, discussing their thinking with other students, presenting their work and having to make sure that it adequately communicates their process, and getting regular, frequent feedback from me are all really helpful for their learning of both the math content and how to be a better student. On the minus side, it means that there isn't much time left for group explorations or as thorough grounding of each lesson as I would like, both in terms of how much class time is available and how much time I have to plan lessons outside of class.
I use this system not because I think it's super duper awesome, but because I haven't seen any other way that accomplishes the student learning piece better. A few things that have helped me be slightly more efficient:
- If I see a bunch of errors, say three or more, I stop grading the paper and write a note to the student reminding them that they need to check their answers and make corrections, either on their own or with help from me. The assignment doesn't get any credit until that happens. I don't want them relying on me to check their answers for them, and I want them to come in and get help.
- As the year continues, I start restricting the amount of time given before corrections can be turned back in to me. Eventually, they are not allowed to correct any more and must come in and get help before turning in the work in the first place. This helps them transition to their future math classes, none of which allow corrections on homework assignments.
- I try not to assign too many problems and assign ones that I think are meaningful and helpful to students' learning. Kids do see the connection between putting effort into their homework and their learning and progress in the class.
But really, this is a crazy inefficient system, especially in terms of my time use. I don't know about everyone else, but grading homework for me is somewhere up there between having hot pokers shoved into my eyes and being trapped in an airless mine shaft. It's seriously obnoxious. But I hate the idea of just grading based on completion because then there's no feedback to the student and much less of a connection between homework and learning. So, I'm stuck with my current system unless someone has any suggestions.
Okay, on to differentiation!!
So I don't currently actively differentiate a lot of homework, other than test corrections and journal entries. There is a good deal of differentiation that happens as a natural outcome of how I structure homework though because students who didn't get full credit on assignments have to correct them, which means that they are addressing their own specific misunderstandings. Also, students who score less than 70% on a test are required to complete extra work as well as meet with me.
Here are some other ideas of things I'd like to try:
- After a quiz, breaking up the class into groups based on the types of mistakes they made. Each group will have all the kids that need to work on a particular concept together. Then, I can work with each group to reteach/address misunderstandings on that topic and their homework will be problems targeting that specific concept. The kids that rocked the quiz will work together on a challenge problem. Their homework will be to complete it and do a write-up of their process.
- In my regular-paced class, which is completing Algebra 1 over two years, we often spend two days on a learning target. For the first day, I'd like to assign everyone the same basic homework assignment. Then, for the second night's homework assignment, students will have the option of either doing more basic practice OR to do a more challenging, shorter set.
- I loved this post by Bob Lochel that I recently read about differentiating homework assignments in which different problems are worth different point amounts (depending on difficulty) and the students complete enough problems of their choice to earn the assigned total point value.
Looking forward to reading everyone else's differentiation strategies and ideas.
Subscribe to:
Posts (Atom)









