Thursday, December 5, 2013
Graphing quadratic functions foldable
Nothing too fancy or mind-shattering here, but perhaps someone may find this useful. Just a quick, little graphic organizer for the steps I want students to follow to make a nice graph of a quadratic function.
Wednesday, December 4, 2013
Group success!!
Today had one of those class periods. You know the ones. Where everyone is working and discussing and arguing and engaged and I'm? I'm just there. Totally and completely unnecessary to the workings of my class. Amaze.
Today was the first day of learning to solve systems by substitution. We went through an example together using @cheesemonkeysf's patented "substitution by stars" method. Then, I passed out some problems for them to work through, telling them to work with their group members and only go to the next problem when everyone in the group was totally good with the previous one. There were some where students had to apply the distributive property and some where they had to isolate a variable first. We had not talked about these. I did not stop class to discuss and fix and give hints, just circulated the room and looked on. Not one kid asked me for help for the 20 minutes that they worked - they puzzled through and argued and made mistakes and erased them and made some more and eventually figured it out all on their own. Holy wow. You guys get it. We all want group work to go exactly like this, but it so rarely does.
Today was the first day of learning to solve systems by substitution. We went through an example together using @cheesemonkeysf's patented "substitution by stars" method. Then, I passed out some problems for them to work through, telling them to work with their group members and only go to the next problem when everyone in the group was totally good with the previous one. There were some where students had to apply the distributive property and some where they had to isolate a variable first. We had not talked about these. I did not stop class to discuss and fix and give hints, just circulated the room and looked on. Not one kid asked me for help for the 20 minutes that they worked - they puzzled through and argued and made mistakes and erased them and made some more and eventually figured it out all on their own. Holy wow. You guys get it. We all want group work to go exactly like this, but it so rarely does.
But finally!! All of the working on norms and redirecting questions with, "Have you asked your group yet?" or "Is this a group question?" and biting my lip to avoid butting in have paid off and there was just this amazing energy and focus and I was so, so proud. Cause there aren't that many glorious classroom moments like this, and it's so easy to focus on all the ways that we aren't perfect and they aren't either. So I want to stop and acknowledge that today was exactly right and keep it in my memory bank for when I'm feeling frustrated and disgruntled. Hooray!!!!
Sunday, December 1, 2013
Axis of symmetry for a quadratic function
My two-year Algebra course is just starting our study of quadratics. So far, we've looked at graphs and tables for quadratic functions and compared them to linear functions and talked about the symmetry of the shape and finding the axis of symmetry from the x-intercepts and finding the reflections of points across the axis of symmetry. I would like students to derive the formula for the axis of symmetry: 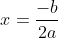 for the quadratic function
for the quadratic function  . The Exeter Math 1 curriculum does this by having students graph functions in the form
. The Exeter Math 1 curriculum does this by having students graph functions in the form  , then generalizing the idea that one of the x-intercepts is zero and the other one is
, then generalizing the idea that one of the x-intercepts is zero and the other one is 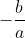 . I created a worksheet that extends on this idea using desmos to graph and having students also derive the formula for the axis of symmetry by averaging the two x-intercepts to get
. I created a worksheet that extends on this idea using desmos to graph and having students also derive the formula for the axis of symmetry by averaging the two x-intercepts to get 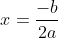 . Then, just like in the Exeter packet, I will have students compare graphs of
. Then, just like in the Exeter packet, I will have students compare graphs of  to graphs of
to graphs of  to realize that the axis of symmetry is not changed by adding a c value to the equation. I'm hoping that the logical progression of the graphs will make sense and that the questions are open enough for this to be genuinely based on student thinking and discovery, but with enough structure that students who are not necessarily used to deriving formulas will have something concrete to think about and answer. Any and all feedback welcome!!
to realize that the axis of symmetry is not changed by adding a c value to the equation. I'm hoping that the logical progression of the graphs will make sense and that the questions are open enough for this to be genuinely based on student thinking and discovery, but with enough structure that students who are not necessarily used to deriving formulas will have something concrete to think about and answer. Any and all feedback welcome!!
Subscribe to:
Posts (Atom)




