Sunday, December 1, 2013
Axis of symmetry for a quadratic function
My two-year Algebra course is just starting our study of quadratics. So far, we've looked at graphs and tables for quadratic functions and compared them to linear functions and talked about the symmetry of the shape and finding the axis of symmetry from the x-intercepts and finding the reflections of points across the axis of symmetry. I would like students to derive the formula for the axis of symmetry: 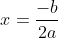 for the quadratic function
for the quadratic function  . The Exeter Math 1 curriculum does this by having students graph functions in the form
. The Exeter Math 1 curriculum does this by having students graph functions in the form  , then generalizing the idea that one of the x-intercepts is zero and the other one is
, then generalizing the idea that one of the x-intercepts is zero and the other one is 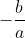 . I created a worksheet that extends on this idea using desmos to graph and having students also derive the formula for the axis of symmetry by averaging the two x-intercepts to get
. I created a worksheet that extends on this idea using desmos to graph and having students also derive the formula for the axis of symmetry by averaging the two x-intercepts to get 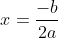 . Then, just like in the Exeter packet, I will have students compare graphs of
. Then, just like in the Exeter packet, I will have students compare graphs of  to graphs of
to graphs of  to realize that the axis of symmetry is not changed by adding a c value to the equation. I'm hoping that the logical progression of the graphs will make sense and that the questions are open enough for this to be genuinely based on student thinking and discovery, but with enough structure that students who are not necessarily used to deriving formulas will have something concrete to think about and answer. Any and all feedback welcome!!
to realize that the axis of symmetry is not changed by adding a c value to the equation. I'm hoping that the logical progression of the graphs will make sense and that the questions are open enough for this to be genuinely based on student thinking and discovery, but with enough structure that students who are not necessarily used to deriving formulas will have something concrete to think about and answer. Any and all feedback welcome!!
Subscribe to:
Post Comments (Atom)
Anna
ReplyDeleteThanks for sharing your work and story. Along these lines - I was at a workshop at Exeter in the summer a few years back. A quadratic presentation urged us to be careful whenever we write the quadratic formula. Rather than write one big fraction, break it up as (-b/(2a)) +/- blah blah blah
This clearly draws your eyes to the axis of symmetry piece of the solution. It re-emphasizes the symmetric relationship between the roots and helps reinforce the fact (later on) that complex roots come in conjugate pairs.
Just another think to think about
Thanks! That's a great point. I definitely emphasize the axis of symmetry equation "hidden" inside the quadratic formula, but I like the idea of writing it as two separate functions for greater emphasis.
DeleteI like your idea. I think that I would have kids factor the quadratic y=ax^2+bx to y=x(ax+b) and find the zeros x=0 and x=-b/a and then say the axis of symmetry is halfway between the two zeros... Maybe... I guess it would depend on the level of the students.
ReplyDeleteDefinitely - I've done it both ways. With students that can abstract it, factoring x out of ax^2 + bx and then using the zero product property totally makes sense. For students that aren't ready for that leap of abstraction, they can usually still "see" the pattern as long as there are numbers in place of the a and b in the equation.
Delete